Electromagnetic Radiation: Field Memo
− FIELD SERVICE MEMO −
ELECTROMAGNETIC RADIATION
and
HOW IT AFFECTS YOUR INSTRUMENTS
May 20, 1990
OSHA Cincinnati Laboratory
(now the Cincinnati Technical Center)
Cincinnati, Ohio
PURPOSE: The purpose of this field service memo is to provide OSHA compliance officers with basic principles of electromagnetic (EM) radiation. It discusses the effects of radio frequency interference (RFI) on the operation of industrial hygiene instruments, explains why special isotropic probes are used for making non-ionizing radiation surveys, and emphasizes the need for special attention in measuring radio frequency fields.
PREFACE: Some discussion of the following subject matter has been simplified for the sake of handling the subject in this limited space.
If this is your first exposure to the subject, some terms and concepts in this memo might be unfamiliar to you. By reading the entire service memo completely at one sitting, some of your initial questions raised in one section may get answered in subsequent sections. Once you make it through the material one time, it is recommended you read the entire service memo over again a second time at another sitting.
CONTENTS
- Waves in General and Electromagnetic Waves
- Units
- Relationship Between Electric and Magnetic Fields
- Propagation of Electromagnetic Energy
- Polarization of the Electromagnetic Fields
- Near-field vs. Far-field
- Electromagnetic Fields and Circuitry
- A Problem for OSHA Compliance And Action Being Taken
- Conclusion
- References
- Appendix A Abbreviations and Symbols Used In This Text
- Appendix B Inverse-Square Law Explanation
- Appendix C Comparing the E = H x 377 Equation with E = I x R
- Appendix D More on Polarization
I. WAVES IN GENERAL AND ELECTROMAGNETIC WAVES:
Electromagnetic radiation is a wave phenomena. Before attempting to understand electromagnetic radiation, let's first review a few properties of waves. A "wave" is a disturbance that is a function of time and/or space. A wave moves through a medium or space and transfers energy from point to point as it moves.
"Wave motion can be thought of as the transport of energy and momentum from one point in space to another without the transport of matter. In mechanical waves, e.g., water waves, waves on a string, or sound waves, the energy and momentum are transported by means of a disturbance in the medium that is propagated because the medium has elastic properties. On the other hand, in electromagnetic waves, the energy and momentum are carried by electric and magnetic fields, which can propagate through a vacuum."
"Although the variety of wave phenomena observed in nature is immense, many features are common to all kinds of waves, and others are shared by a wide range of wave phenomena.[1]
The "size" or "height" of a water wave is called its amplitude and tells us of its strength. All waves can be described in reference to their "amplitude" or "strength". As a wave travels (propagates) out from the source, the total energy radiated from the source remains the same, but the strength of the wave decreases as the distance from the source increases. A classic two dimensional example shows the ripple rings expanding out from a disturbance over the surface of a calm pond. Three dimensional waves require going one step farther by imagining expanding spheres instead of expanding rings. As the wave travels from the center disturbance, the wave energy is spread out thinner over larger areas, resulting in less energy per unit area, thus decreased "strength". The total energy stays the same, but it is distributed over a larger area.
Now let's "switch gears" and look at another property of waves. If we could observe a wave as it passes by a point in space, we would notice the amplitude of the wave changing with time in a periodic or cyclical manner. Because a wave is periodic, we can count the number of complete wave cycles that pass by that point each second. This would be the "frequency" of the wave.
"Frequency" is measured in Hertz (Hz), wave cycles per second. All waves are composed of at least one sine wave or frequency element. Waves that have non-sinusoidal looking waveforms are actually a combination of two or more sine waves of different frequencies
NOTE: Mathematics shows us that every wave shape is actually a combination of individual sine waves of different frequencies. A whole area of mathematics called "Fourier Analysis" is dedicated to analyzing the sinusoidal component frequencies of waveforms.
Electromagnetic radiation is a wave phenomena and has all of the above qualities of waves. An electromagnetic (EM) wave can be defined as a "wave characterized by variations of electric and magnetic fields".[2] EM waves can travel through space while carrying energy at the speed of light. Many people think of them simply as radio waves, but EM waves cover a much broader frequency spectrum. EM waves extend from the very lowest frequency (Hz) to frequencies beyond radio waves, light waves, X-rays, and gamma rays.[1] This broad energy range is know as the electromagnetic spectrum. Depending on their frequency, EM waves are known as radio waves, heat rays, light rays, etc. In this field service memo, we will be mostly concerned with radio waves ranging from 10 kHz to 3 GHz. A diagram of this portion of the spectrum is shown in Section VIII, Figure 2.
While radio frequency EM waves are intentionally generated by cellular phones, walkie talkies, garage door openers, radio stations, and television (TV) stations, they are unintentionally generated by electric motor brushes, ignition systems of gasoline engines, medical equipment, computer systems, and lightning. Even the sun produces radio frequency electromagnetic radiation. The effects of unintentionally generated EM waves will be discussed in Section VII and Section VIII.
II. UNITS:
All electromagnetic fields (EM waves) consist of two component fields, electric fields (E fields) and magnetic fields (H fields). E fields and H fields are companions and together make up the total EM field. Where one is, so is the other. Electric field strength (E) is measured in units of volts per meter (V/m). Magnetic field strength (H) is measured in amperes per meter (A/m).
Power is the time rate of energy transfer. This applies to waves, too. Radiated power is that power given off by a radiation source (antenna) and carried through space by the EM wave. Power is measured in watts (W). Power density is the amount of power distributed over a given unit area perpendicular to the direction of travel. Power density is expressed in watts per square meter (W/m2) or milliwatts per square centimeter (mW/cm2).
EM radiation is a periodic wave motion. The number of repetitions of the waveform, or cycles per second, is called the frequency and is measured in Hertz (Hz). 1 kilohertz (kHz) = 1000 Hz, 1 megahertz (MHz) = 1 million Hz, 1 gigahertz (GHz) = 1 billion Hertz, 1 terahertz (THz) = 1 trillion Hertz, etc.
Related to frequency is the term wavelength. It is the distance a wave travels during the time period of one complete oscillation cycle. The wavelength of an EM wave is the wave's speed of travel (usually the speed of light) divided by the frequency of the wave. The symbol for wavelength is λ (Lambda). It is measured in units of length, such as meters, centimeters, angstroms, feet, etc. The table on the next page shows the wavelength (λ) of certain frequencies (f) when the speed of transmission is the speed of light (C), 300,000,000 meters per second (186,280 miles per second). λ = C/f.
| FREQUENCY (f) | WAVELENGTH (λ =C/f) |
|---|---|
| 1Hz | 186,280 miles (300,000 km) |
| 10Hz | 18,628 miles (30,000 km) |
| 60Hz | 3105 miles (5,000 km) |
| 1000Hz (1 kHz) | 186.4 miles (300 km) |
| 10kHz | 18.6 miles (30 km) |
| 100kHz | 9836 feet (3,000 meters) |
| 1000kHz (1 MHz) (AM radio) | 984 feet (300 meters) |
| 10MHz | 98.4 feet (30 meters) |
| 27MHz (many RF sealers) | 36.4 feet (11 meters) |
| 30MHz | 32.8 feet (10 meters) |
| 100MHz (FM radio) | 9.8 feet (3 meters) |
| 300MHz | 3.28 feet (1 meter) |
| 1000MHz (1GHz) | 11.8 inches (30 cm) |
| 2.45GHz (Microwave ovens) | 4.8 inches (12.2 cm) |
| 10GHz (Satellite data links) | 1.18 inches (3 cm) |
III. RELATIONSHIP BETWEEN ELECTRIC AND MAGNETIC FIELDS:
Understanding electromagnetic field relationships is difficult, but compliance officers are faced with measuring these fields. It is critical for us to know and understand what the EM field components are and the relationship between them so that meaningful measurements and accurate data are taken.
As mentioned earlier, electromagnetic fields (EM waves) are composed of two types of fields, electric fields and magnetic fields. The relationship of electric fields to magnetic fields can be compared to the relationship between voltage and current in a simple electric circuit. The electric (E) field is much like the electric voltage potential (E) of an electric circuit. The magnetic (H) field is much like the electric current (I) of an electric circuit.
NOTE: In this text, the symbol "E" usually refers to the electric field component of an EM field. In a few cases where it is used for electric voltage potential "E", it will be specifically identified and will usually be accompanied by "I" (electric current).
Electric voltage potential and electric current are measured in volts and amperes respectively; E fields and H fields are measured in volts per meter and amperes per meter, respectively. Where there is electrical current flowing, there also is a voltage associated with it. Where there is an H field, there also is an E field associated with it.
The complete mathematical relationship between E fields and H fields is complicated and involves terms expressed in 4 dimensions. The complete mathematical picture is too involved for this field service memo. However, most applications allow for the math terms to be reduced to simple formulas.
Under the simple conditions of wave travel through free space, the relationship of electromagnetic fields is reduced to:
E = H x 377 (Under free space conditions.)
where E = the electric field strength,
377 = the characteristic impedance of free space,
H = the magnetic field strength,
√(μv /εv) a constant with units expressed in Ohms.
The equation for electromagnetic waves in free space, E = H x 377, and the equation for Ohm's Law, E = I x R, are very similar. Both equations are special case simplifications of some very complex mathematical statements defining electromagnetic theory. Fortunately, some very intelligent men have reduced this math into a few simple formulas like these, which we can use under certain ordinary conditions. Three of these men are Maxwell, Gauss, and Ohm. Thanks to them, we don't have to be expert mathematicians to make electromagnetic surveys. If you are familiar with Ohm's law, Appendix C, "Comparing the E = H x 377 Equation with E = I x R," may be helpful in understanding the electromagnetic field equation given above.
As an electromagnetic wave travels through space, energy is transferred from the source to other objects (receivers). The rate of this energy transfer depends on the strength of the EM field components. Keeping it simple, the rate of energy transfer per unit area (power density) is the product of the electric field strength (E) times the magnetic field strength (H).
Pd = E X H
Watts/meter2 = Volts/meter X Amperes/meters
where Pd= the power density, E = the electric field strength in volts per meter, H = the magnetic field strength in amperes per meter.
The above equation yields units of W/m2. The units of mW/cm2 are more often used when making surveys. One mW/cm2 is the same power density as 10 W/m2 The following equation can be used to obtain these units directly:
Pd = 0.1 x E x H mW/cm2
The simple relationships stated above apply at distances of about two or more wavelengths from the radiating source. This distance can be a far distance at low frequencies, and is called the far field. Here the ratio between E and H becomes a fixed constant (377 Ohms) and is called the characteristic impedance of free space. Under these conditions we can determine the power density by measuring only the E field component (or H field component, if you prefer) and calculating the power density from it.
We take advantage of this fixed relationship when we measure potentially hazardous EM fields during an RF hazard survey. Exposure hazards that are due to absorption by the human body are ultimately evaluated with respect to the actual energy absorbed. Since power is the rate of energy transfer, and the squares of E and H are proportional to power, E2 and H2 are proportional to the energy transfer rate and the energy absorbed by the subject. Because compliance officers find it convenient to measure EM fields in terms of E2 and H2 survey meters usually readout in terms of E2 or H2.
Electromagnetic field exposure limits which were set for human exposure are listed in ANSI C95.1-1982[4] as Radio Frequency Protection Guides (RFPG). There, values for electromagnetic field levels are listed in terms of E2, H2 and equivalent power density. These values are based on the rate of energy absorbed into the human body. The term Specific Absorption Rate (SAR) is used in the standard to describe this absorption rate. There is a very good discussion of SAR measurements in ANSI C95 (1990)[5]. More discussion of SAR will be presented in a follow-up field service memo which will be issued at a later date, "Measurement Practices for Non-ionizing Radiation Surveys".
IV. PROPAGATION OF ELECTROMAGNETIC ENERGY:
Most people, including most electrical engineers, think of electricity as electrons flowing in a wire, much like water flowing in a hose. The idea of electrical energy moving through free space in a wave is a completely foreign concept. Yet, electromagnetic radiation is exactly that, electrical energy moving through space as a wave, and electrical energy in a wire is a special case in which the energy is guided by a wire. Some of the energy is internal to the wire, and some of the energy is external to the wire. When we plug an appliance into the receptacle, the power delivered to the appliance does not actually "go through the cord", but is electromagnetic energy being "guided" by the electron activity in the power cord. The electromagnetic energy delivered to the load is external to the wire. The electron activity oscillating back and forth in the wire is a result of the external electromagnetic energy and in turn serves as a way of telling the electromagnetic wave to follow the wire. The electron movement in the wire is proportional to the strength of the wave being guided. Don't be disturbed if you have difficulty grasping this concept. Even engineering students have difficulty understanding it.
Fortunately, to analyze and solve most problems in DC and low frequency AC circuits, it is sufficient to apply the simple Ohm's law equation. Normally it does not require thinking in terms of electromagnetic fields. Low frequency electromagnetic field theory is typically applied only when analyzing the coils of relays, inductors, transformers, and motors. Electromagnetic wave theory becomes more important as frequency climbs into the Megahertz range, such as in analyzing wireless electromagnetic energy transmission, radio frequency circuits, light wave analysis, etc.
EM waves can travel without the guiding action of wires. The points where EM waves leave the guiding influence of wires and move to free and unbounded travel are called antennas. Antennas act as coupling points for electromagnetic energy to leave the guidance of wires for free space, and visa versa. The area near this coupling activity is exactly where compliance officers have to deal with electromagnetic fields, as in the case of RF heat sealers. In general, an antenna might be one of the conductors in an electronic circuit, a metal object such as your front porch railing, or even nonmetallic objects like a tree limb or an extended arm. The effectiveness of an antenna to transmit or receive EM waves depends on the conductivity of the material used, the antenna's shape, and the physical dimensions of the antenna relative to the wavelength of the EM field.
The best broadcast and reception of EM waves is obtained when the dimensions of the antenna properly match the wavelength of the electromagnetic field. That is why the length of TV "rabbit ear" and "whip" antennas need adjustment each time the channel is changed, and why roof mounted TV antennas have so many different sized elements.
When measuring worker exposure to non-ionizing radiation (EM fields), it is important to be aware that the probe is also an antenna. The antenna and circuitry of an RF probe are arranged so it can function over a range of operational frequencies. The width of this operational frequency range is called the bandwidth. If measurements are attempted outside the probe's frequency range, the measurements will be inaccurate and could severely damage the probe. Always choose the proper probe based on both power rating and the frequency.
V. POLARIZATION OF THE ELECTROMAGNETIC FIELDS:
Polarization is another important concept to keep in mind when making electromagnetic measurements. Polarization explains why walkie talkie antennas need to be pointed in the same direction to get best reception and why the probes of RF survey meters must be rotated while you are making measurements.
It should suffice here to define polarization as a characteristic of radiated EM waves which deals with the direction and amplitude relationship of the E field "vector" in relation to the direction of travel.
NOTE: A vector is a mathematical representation of a force or other quantity in terms of both direction and strength.
It is because of this characteristic that we usually use an "isotropic" probe as the receiving antenna when performing a non-ionizing radiation survey. An isotropic probe receives electromagnetic signals regardless of polarization or direction of travel. An isotropic probe is designed to give the same reading, no matter which way it is pointed in the EM field.
Since no probe is perfectly isotropic, survey probes should be rotated about the axis of its handle during measurements (use a rotating wrist motion like you would to turn a door knob). An average of the minimum and maximum reading is used as the reading value.
EM wave reflections caused by metal beams, gratings, etc. can cause a phenomenon called "multipath interference". The reflected wave can have different polarization than the original wave. This can have significant interference impact on the measurement results as the probe is moved from point to point. Therefore, it is good practice not only to rotate the probe, but also to move the probe about in a circular pattern to obtain a general sampling of the area. As the measurements are made closer to the radiating source, it is even more important to carefully survey the general area to find any such localized radiation beams.
Polarization is discussed in greater detail later in Appendix D, "More on Polarization."
VI. NEAR-FIELD VS FAR-FIELD:
Certain behavior characteristics of EM fields dominate at one distance from the radiating antenna, while a completely different behavior can dominate at another location. Electrical engineers define boundary regions to categorize behavior characteristics of electromagnetic fields as a function of distance from the radiating source. These regions are: the "Near-Field", "Transition Zone", and "Far-Field". The regional boundaries are usually measured as a function of the wavelength. Figure 1 shows these regions and boundaries.
Two things should be stressed: these regions categorize behaviors which vary even within each region; and the boundaries for these regions are approximate "rules of thumb" (more precise boundaries can be defined based primarily on antenna type and antenna size, and even then the experts differ).
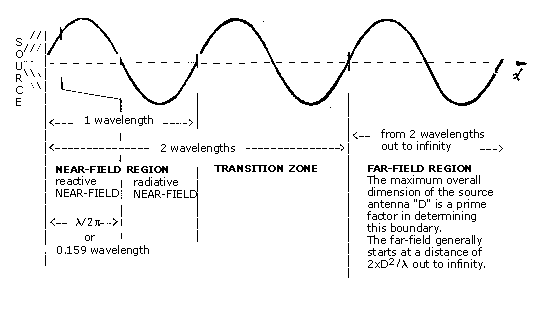
FAR-FIELD: The region extending farther than 2 wavelengths away from the source is called the "Far-Field". In the far-field, E, H, and power density are related by the equations: E = H x 377 and Pd = E x H. These equations were explained in Section III. Combining these two equations together we get:
Pd = H2 x 377 and Pd = E2÷377
where Pd = the power density in watts per square meter (one W/m2 is equal to 0.1 mW/cm2),
H2 = the square of the value of the magnetic field in amperes squared per meter squared,
E2= the square of the value of the electric field in volts squared per meter squared.
The above equations show that in the far-field, all you really need to measure is the E field, actually E2. From this measurement, the power density and value of the H field can be calculated. For reasons explained in Section III, health compliance measurements are more convenient to evaluate when they are measured in terms of the square of the field strength.
TRANSITION ZONE: The region between the near-field and the far-field is called the "Transition Zone". It has a combination of the characteristics found in both the near-field and the far-field. Here it may not always be necessary to measure both E and H to obtain a good approximation of the EM field, but several measurements are needed to characterize the field.
NEAR-FIELD: The region located less than one wavelength from the source is called the "Near-field". Here, the relationship between E and H becomes very complex, and it requires measurement of both E and H to determine the power density. Also, unlike the far-field where EM waves are usually characterized by a single polarization type (horizontal, vertical, circular, or elliptical), all four polarization types can be present in the near-field.
Since both the E field and the H field components of electromagnetic waves are absorbed by living tissue, and since the relationship between E and H is complicated in the near-field, we must measure both E and H when evaluating near-field hazards. This includes all low frequency sources, such as RF heat sealers.
The near-field is further divided into the "reactive" near-field and the "radiative" near-field. The outer boundary of the reactive near-field region is commonly considered to be a distance of 1/2π times the wavelength (λ/2π or 0.159 x λ) from the antenna surface. The radiative near-field covers the remainder of the near-field region, from λ/2π out to λ (one full wavelength).
In the reactive near-field (very close to the antenna), the relationship between the strengths of the E and H fields is too complex to predict. Either field component (E or H) may dominate at one point, and the other way dominate at a point only a short distance away. This makes it extremely difficult to find the true power density there. Not only would E and H both have to be measured, but a new term called the phase relationship between E and H is needed. Present survey meters (such as OSHA's Narda and Holaday units) measure only the magnitude E or H, not this phase relationship. Although it would be very helpful to know the true power density, our present compliance efforts do not require us to determine it. During a compliance survey, both the E field and the H field components are measured separately, read from the meter as E2 and H2 quantities, and each quantity is compared individually against the Radio Frequency Protection Guides (RFPG) of the ANSI C95.1-1982 standard. If either the E field or the H field component exceeds the limits of the RFPG, the level is considered high.
As you might have guessed, the reactive near-field region has another surprise in store for you. In this reactive region, not only is the EM wave being radiated outward into space, but there is a "reactive" component to the EM field. Very close to the antenna, energy of an unknown amount is held back and is stored very near the antenna surface. This reactive component can be the source of confusion and danger in attempting measurements in this region. In other regions the power density is inversely proportional to the square of the distance from the antenna. In the vicinity very close to the antenna, the energy level can rise dramatically with only a small additional movement towards the antenna. This energy can be very dangerous (even hazardous) to both humans and measurement equipment where high powers are involved.
CAUTION: When the radiating dimensions of the antenna are much smaller than one wavelength and/or the frequency is low (as with heat sealers), it is especially important to be aware of the POTENTIALLY HAZARDOUS REACTIVE FIELDS WHICH MAY EXIST IN THE REACTIVE NEAR-FIELD. Exercise extreme caution for both your safety and the equipment when making near-field measurements, in the case of heat sealing machines. As you move nearer to the antenna in the reactive near-field, the energy can increase much quicker than what is computed by the inverse-square law. Some electromagnetic energy is stored in the near-field in the vicinity of the antenna that can be an unsuspected source of dangerous energy. This "reactive field" energy is especially dangerous with high power systems. The closer to the radiating source you get, the more caution should be exercised.
The radiative near-field does not contain any reactive field components from the source antenna. The energy is all radiant energy. As you move further out into the radiative near-field (one half wavelength to 1 wavelength from the source), the E and H field relationship does not have so many surprises as in the reactive near-field, but the E to H relationship is still complex. Since the radiative near-field is still part of the near-field, caution should still be exercised in relation to personal safety and equipment safety. Metal objects such as steel beams can act as antennas by receiving and then "re-radiating" some of the energy, forming a new radiating surface to consider. Not only does this new radiating surface have its own near-field regions, the energy levels might be shockingly high. Exercise caution near such metal objects.
All near-field readings require special attention. In general, readings taken closer than one wavelength require measurement of both the E and H fields. A good general rule of thumb is "Measure the E field above 300 MHz and measure both-the E field and the H field below 300 MHz". For example, when surveying radio frequency heat sealer machinery at 27 MHz (λ = 11.1 meters, or 36.4 feet), both E and H must be measured, since the measurement is in the near-field. Two wavelengths at 27 MHz is 22.2 meters (72.8 feet) away.
While taking measurements in the near-field, you may notice the values for E and H vary considerably from point to point. A very strong E or H field strength may exist only inches away from a very weak E or H field strength. When attempting "power measurement" in the near-field, make an effort to take both the E field and the H field measurements at the exact same physical location, especially if unusual peaks and valleys are observed from point to point. The variation may be only centimeters apart or may be as much as one meter. How much care to be taken will be obvious to you by observing the meter display for abrupt changes.
NOTE: Throughout this section the boundaries for the near and far-field regions have been defined only in terms of wavelength. Actually, the boundaries are based on more. The maximum overall dimension (D) of the radiating antenna is a prime factor in determining these boundaries. This dimension is a physically measured length. Above we assumed that "D" was one wavelength or less. For antennas like the ones mounted on houses for TV (dipole antennas), "D" would be the length of the radiating arm; and for a radar set or heat sealer, "D" might be the maximum dimension of the port opening (or aperture) through which the EM wave passes.
In most situations "D" is between one-fourth to one whole wavelength (λ) long, but there are some situations where "D" might be much larger or much smaller than "λ". When "D" is much larger 2 than "λ", the far-field boundary is not 2λ as shown in figure 1, but is 2 D2 /λ.
Far-field boundary = 2 D2/λ
where D = the largest radiating dimension of the antenna
λ = (lambda) one wavelengthTherefore, if the maximum overall dimension exceeds "λ", the far-field boundary extends farther out than 2λ. Thus we might be required to measure both the E and H field components, even beyond the 2λ> distance or when the frequency is above the 300 MHz "rule of thumb". But don't panic, these situations are usually the exception, but you should be aware of their existence.
More commonly, an antenna may be such that the maximum overall dimension (D) is much less than one wavelength. In these cases, the "radiative" portion of the near-field region may not even exist at all. However, the nastier "reactive" near-field still exists, and it extends out to X/2π from the source. So, even in cases where "D" is much less than "λ", it is best to follow the "rule of thumb" practice of measuring both the E field and H field for frequencies below 300 MHz.
The boundaries shown in Figure 1. should not to be considered rigid, but they are values obtained by consensus to help categorize wave motion characteristics and behavior into regions. Characteristic behavior expressed in one region is not fully excluded from existing to a lesser extent in an adjacent region. The multiple characteristics of the transition zone are a prime example of overlapping behavior. The regional boundaries primarily indicate where certain characteristics require special attention.
Perhaps in a summary we can best look at two examples. The far-field for microwave oven emissions at 2.45 GHz is only inches from the source, so it is sufficient to measure only the E field. However, for radio frequency (RF) heat sealers operating at 27 MHz, both E and H must be measured, because we are in the near-field. Even when "D" is very small, the "reactive" near-field boundary of λ/2π at 27 MHz is 1.77 meters (5.8 feet). Thus RF heat sealers and all near-field measurements require special attention to both field components.
VII. ELECTROMAGNETIC FIELDS AND CIRCUITRY:
This section describes two related topics, electromagnetic interference (EMI) and electromagnetic susceptibility (EMS). The term EMI is mostly used to describe electrical signals that are given off from one source and interfere with the operation of another electronic appliance. Comparing with sound waves, music to one person can be noisy interference to someone in the next room. EMS deals with the way EMI disrupts the normal operation of the victim appliance.
OSHA's compliance instruments are small, light-weight, and battery operated appliances. To achieve light weight, they use small batteries and low-power circuits. Some of the circuits use analog signals (voltages and currents of varying amplitude) and some are digital (voltage pulses to indicate 1's and 0's). When low power levels are used in either of these circuits, they become more susceptible to interference from external electromagnetic fields.
The universe is full of EM fields, and they are constantly mixing with the EM fields that are operating our electronic circuits. When the external field induces signals in an instrument's circuits that are significant in relation to normal circuit signals, interference results. As the strength of the interfering field increases and the power level of the instrument's circuitry decreases, the probability of unwanted responses increases significantly. The interference can cause erroneous data, unwanted results, false alarms, or even complete shutdown of the instrument. The effects can be totally unpredictable. Adequate electromagnetic protection is being recognized as a critical element in design of low power equipment.
To protect against EMI, circuits are sometimes shielded in metal enclosures, called electromagnetic shielding. Shielding is also used to prevent EMI from radiating out from the source. Parts of a stereo system handling low level signals are shielded to keep out the 60 Hz hum of power lines. Large computers are shielded to prevent the electromagnetic fields from radiating and causing interference in other equipment. Sometimes additional circuitry, called EMI filters, are added to redirect unwanted signals away from sensitive circuitry. Typically, EMI filters are built into the equipment circuitry.
A circuit's susceptibility to interfering radio waves is referred to as its Electromagnetic Susceptibility (EMS). Instruments showing no effect from signals at one frequency may behave totally different at another. The instrument's physical circuit dimensions, electrical characteristics, and shielding all influence the frequency dependency of an instrument's EMS performance. Often manufacturers take little or no concern about EMI and EMS until someone complains of problems well after production has begun. Both EMI and EMS problems can be solved by good design, sufficient testing, and proper safeguards by the user.
VIII. A PROBLEM FOR OSHA COMPLIANCE AND ACTION BEING TAKEN:
Veteran compliance officers will agree that EMS has not been a significant problem with older instruments. The circuitry operated at power levels high enough that the effects of external fields were not noticed. OSHA's newer instruments consume less power and are more portable, but are more likely to be susceptible to EMI. EMI problems were experienced with the original purchase of DuPont Mark 1 dosimeters and caused 400 units to be recalled and modified. To avoid having another such recall, instruments are now being thoroughly tested by the Cincinnati Laboratory for EMS before purchase. Examples of instruments recently tested are audiodosimeters, combustible gas meters, air sampling pumps, and air velocity meters.
As a result of this testing, many manufacturers have become aware of EMS and have begun designing instruments to reduce the susceptibility. However, EMS is still not getting proper attention by some manufacturers of industrial hygiene instruments. Some instruments show degraded performance when exposed to EM field strengths as low as 0.01 mW/cm2. By comparison, the OSHA worker safety standard of the 1970's is 10 mW/cm2, and the ANSI C95.1-1982 standard is 1 mW/cm2 for frequencies of greatest concern to us. While non-ionizing radiation levels in violation of this OSHA standard are not very common, the lower levels found to effect some industrial hygiene instruments are more common. It is reasonable to expect OSHA's instruments will be exposed to these levels. Figure 2. graphically shows these levels.
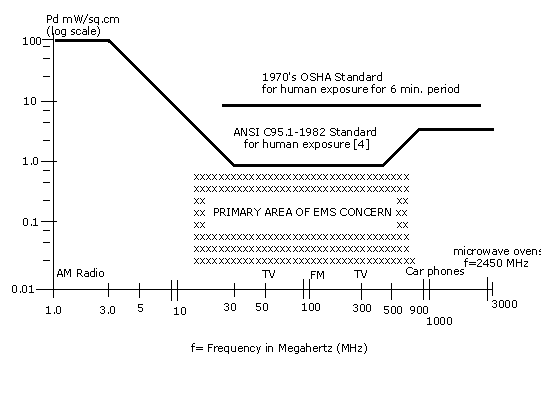
In the presence of an electromagnetic field, degraded instrument performance shows itself as anything from subtle deviations to gross errors, or even complete failure of the instrument. Symptoms of interference may include: false alarming of the instrument, changes in reading with no obvious cause, intermittent failures, illogical displays, etc. Even when these obvious symptoms are absent, EMS caused errors can still degrade the accuracy of the instrument readings.
To assure OSHA's new instruments meet minimum criteria for EMS susceptibility, the OSHA Cincinnati Laboratory performs EMS tests on portable instruments being considered for purchase by OSHA. This is part of the laboratory's equipment evaluation program. Existing equipment is also scheduled for EMS testing to verify accurate performance. This testing is done in a special chamber called a Transverse Electromagnetic (TEM) Cell.
IX. CONCLUSION:
Congratulations! You have now reached the end. Hopefully this explanation has provided you with a better general understanding of electromagnetic (EM) waves and susceptibility to unwanted electromagnetic waves. The topics are not easy, and require complex mathematics to better understand them.
A follow up field service memo, to be issued at a later date, will describe "Measurement Practices for Non-ionizing Radiation Surveys". It will apply the information of this memo to the task of taking actual field measurements of potentially hazardous radio frequency electromagnetic fields.
X. REFERENCES
[1] Tipler, Paul A., Physics, Worth Publishers, Inc., 1982, Page 396.
[2] ANSI/IEEE 100-1984, IEEE Standard Dictionary of Electrical and Electronics Terms, 1984, page 305.
[3] Clayton, George D. and Florence E., Patty's Industrial Hygiene and Toxicology, John Wiley & Sons, New York, 1978, Page 448.
[4] ANSI/IEEE C95.1-1982, "American National Standard Safety Levels with Respect to Human Exposure to Radio Frequency Electromagnetic Fields, 300 kHz to 100 GHz", 1982.
[5] ANSI C95.3(1991) "American National Standard Recommended Practice for the Measurement of Potentially Hazardous Electromagnetic Fields - RF and Microwave".
APPENDIX A
ABBREVIATIONS AND SYMBOLS USED IN THIS TEXT
Å
Angstrom, unit of length, one ten billionth of a meter (0.0000000001), used only in Figure 1
on page 3. All other uses of the abbreviation "A" in this text refer to "Amperes".
A
Amperes, unit of electrical current
AC
Alternating Current
A/M
Amplitude modulated, also the frequency band of commercial radio extending from 535
kHz to 1605 kHz
E
Electric voltage potential (When "E" is used for electric voltage potential in this text, it well
identified as such. All other uses of "E" in this text represent Electric field component of
EM fields.
E/M
Ratio of the electric field (E) to the magnetic field (H), in the
far-field this is the characteristic impedance of free space, 377 Ohms.
EM
Electromagnetic
EMI
Electromagnetic Interference
EMS
Electromagnetic Susceptibility
FM
Frequency modulated, also the frequency band of commercial radio extending from 88 MHz to 108 MHz
GHz
Gigahertz, one billion Hertz (1,000,000,000 Hertz)
H
Magnetic, In this text, unless otherwise identified, "H" is the magnetic field component of an electromagnetic field.
Hz
Hertz, unit of measurement for frequency (cycles per second)
I
Electric current
kHz
Kilohertz, one thousand Hertz (1000 Hertz)
;λ
Lambda, symbol for wavelength, distance a wave travels during the time period necessary for one complete oscillation cycle
MHz
Megahertz, one million Hertz (1,000,000 Hertz)
µm
Micrometer, unit of length, one millionth of an meter (0.000001 meter)
m
Meter, the fundamental unit of length in the metric system
mil
Unit of length, one thousandth of an inch
mW
Milliwatt (0.001 Watt)
mW/cm2
Milliwatts per square centimeter (0.001 Watt per square centimeter area), a unit for
power density, one mW/cm2 equals ten W/m2
nm
Nanometer, one billionth of a meter (0.000000001 meter)
OSHA
Occupational Safety and Health Administration
Pd
Power density, unit of measurement of power per unit area (W/m2 or mW/cm2)
R
Resistance
RF
Radio Frequency
RFI
Radio Frequency Interference
RFPG
Radio Frequency Protection Guides, as listed in Table 1 of ANSI Standard C95.1-1982
SAR
SPECIFIC ABSORPTION RATE, as described in of ANSI Standard C95.1-1982
THz
Terahertz, one trillion Hertz (1,000,000,000,000 Hertz)
TV
Television, also the frequency band of commercial broadcast extending from 54 to 72
MHz, 76 to 88 MHz, 174 to 216 MHz, and 470 to 806 MHz
V
Volts, unit of electric voltage potential
V/m
Volts per meter, unit of electric field strength
V2/m2
Volts squared per meter squared, in this text it is the quantity of electric field strength multiplied by itself (volts per meter, quantity squared)
W/m2
Watts per square meter, a unit for power density, one W/m2 equals 0.1 mw/cm2
Ω
Ohms, unit of resistance
APPENDIX B
INVERSE-SQUARE LAW EXPLANATION
In Section I, it was said that all waves can be described in reference to their "amplitude" or "strength". As a wave propagates out from the source, the total energy radiated from the source remains the same, but the strength of the wave decreases as the distance from the source increases.
Although much like the classic two dimensional example of ripple rings expanding out over the surface of a pond, three dimensional waves require going one step farther. Instead of expanding rings, we can imagine expanding "spheres" spreading out from the source as the wave travels from the center disturbance (sort of like concentric balloons being inflated). The wave energy is spread out over larger and larger areas as the radius increases, thus resulting in less energy per unit area, decreased "strength". Because the surface area of a sphere is 4 π , the area of a sphere increases in proportion to "r2", and energy which is equally spread out over the surface is inversely proportional to "r2". This is known as the inverse-square law.
The inverse-square law is defined as: "A statement that the strength of a field due to a point source or the irradiance from a point source decreases as the square of the distance from the source. Note: For sources of finite size this gives results that are accurate within one-half percent when distance is at least five times the maximum dimension of the source (or luminaire) as viewed by the observer." [B1]
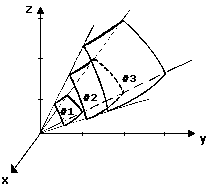
Consider a wave propagating outward into the 3 dimensions of space, with a given surface expanding as it travels away from the radiating source. The surface area balloons like an expanding sphere. The area increases in pro-portion to the square of the distance from the wave source (except in cases using parabolic dish antennas, such as radar or satellite dishes). Since the total energy remains constant, the energy per unit area (or energy density) decreases. Thus the measured strength of a wave decreases as the wave propagates through space and is spread out over larger and larger areas. As a single receiving object moves farther from the radiating source, less energy is transmitted between the two objects.
The inverse-square law would make long distance space communications impossible, but parabolic dish antennas were developed to reshape and redirect the expanding sphere-like propagation into a narrow beam. Most ordinary industrial hygiene applications do not involve parabolic antennas (often called satellite dishes), and an inverse-square law type of relationship can normally be assumed.
REFERENCES
[B1] ANSI/IEEE 100-1984, IEEE Standard Dictionary of Electrical and Electronics Terms, 1984, page 464.
APPENDIX C
COMPARING THE E = H x 377 EQUATION WITH E = I x R
In Section III, we discussed the relationship between electric and magnetic fields. Because compliance officers are faced with making measurements of these fields, it is critical to understand the basics of the relationship between E, H, and power density. This appendix discusses the relationship in more detail by comparing E = H x 377 with its cousin E = I x R, Ohm's law.
The E field is much like the electric voltage potential (E) of electric circuits, and the H field is much like the electric current (I) of electric circuits. In electric circuits we measure E and I in units of volts and amperes, respectively; E fields and H fields are measured in volts per meter and amperes per meter, respectively. Where electrical current flows, there also is a voltage associated with it. Where there is an H field, there also is an E field associated with it.
The equation for electromagnetic waves in free space, E = H x 377, and the equation for Ohm's Law, E = I x R, are very similar. Both equations are special case applications of some very complex mathematical statements defining electromagnetic theory. During the 18001s, mathematicians and scientists formulated equations to express the mathematical relationships associated with electromagnetic waves. These equations predict the behavior of EM waves. Three men who were major contributors to this work are K.F. Gauss, G.S. Ohm, and James Clerk Maxwell. Hertz later verified Maxwell's work experimentally. By applying specific conditions, such as for an EM plane wave traveling through free space, formulas like E = H x 377 flow from the more complicated math. E = I x R applies the principles to conducting mediums (electric circuits). (Most text books on electromagnetic wave theory, such as Jordan and Balmain's book listed as reference[C1], discuss this in great detail.)
Under simple free space conditions, Maxwell's equations can be reduced to:
E = H x 377 (Under free space conditions.)
and Pd = E x H W/m2 or Pd = 0.1 x E x H mW/cm2
where E = the electric field strength in Volts/meter,
H = the magnetic field strength in Amperes/meter,
377 = the characteristic impedance of free space, Z0
Pd = the power density in W/m2 or mW/cm2 as appropriate.
Under simple circuit conditions at low frequencies, the following equations apply:
E = I x Z or E = I x R (when Z is resistive)
and P = E x I Watts (when Z is resistive)
where E = the electric voltage potential in Volts,
I = the electric current in Amperes,
Z = the circuit impedance (resistive and reactive) in Ohms,
R = the circuit resistance in Ohms,
P = the power in Watts.
The similarities between the Ohm's law for electric circuits and free space conditions for EM fields are obvious when compared side by side:
| Circuits | EM Fields |
|---|---|
| Voltage potential (E), Volts | Electric field strength (E), Volts/meter |
| Electric current (I), Amperes | Magnetic field strength (H), Amperes/meter |
| Circuit Impedance (Z), Ohms | Characteristic Impedance (Z), Ohms |
| Circuit Resistance (R), Ohms | Impedance of free space (Zo=377), Ohms |
| E = I x Z Volts | E = H x Z Volts/meter/ |
| When Z = resistive: | When in the far-field, Zo = 377 Ohms: |
| E = I x R Volts | E = H x 377 Volts/meter |
| and P = E x I Watts | and Pd = E x H Watts/meter2 |
| Substituting for E and I: | Substituting for E and H: |
| P = I2 x R Watts | Pd = H2 x 377 Watts/meter2 |
| P = E2/R Watts | Pd = E2 /377 Watts/meter2 |
The above comparison may help you better understand the relationship between E fields and H fields, if you already are familiar with electric circuit theory.
The simple free field relationships stated above apply at distances of about two or more wavelengths from the radiating source, called the far-field. Here Z (the ratio of E to H) is a fixed constant equal to 377 Ohms, and here we can determine the power density by measuring only the E field (or H field) and then calculate the power density from it. Survey meters usually readout in terms of E2 or H2 Power density is E2 divided by 377 or is H2 times 377 under these conditions.
NOTE:The above does not apply when dealing in the near-field, because in the near-field Z is not usually equal to 377 Ohms or anything close to it. In fact, in the near-field, Z can have any value from 0 to infinity, and can change very quickly from one measurement position to another. That is why both E and H must be measured when we are making measurements in the near-field.
REFERENCES
[C1] Jordan, Edward C. and Balmain, Keith G., Electromagnetic Waves and Radiating Systems, Prentice-Hall, Inc., 1968, Pages 103, 118, & 120.
APPENDIX D
MORE ON POLARIZATION
Polarization is an important concept in making electromagnetic measurements. It explains why walkie talkie antennas need to be pointed in the same direction to get best reception and why RF survey probes must be rotated during measurements.
Polarization of a radiated wave is "That property of a radiated electromagnetic wave describing the time-varying direction and amplitude of the electric field vector: specifically, the figure traced as a function of time by the extremity of the vector at a fixed 1 location in space, as observed along the direction of propagation."[D1]
The above definition can be confusing. The following discussion can be used to lessen that confusion and give you a better feel of this important concept
Radiated EM waves traveling through space have a property called polarization. It effects the compatibility of waves and certain types of antennas. There are several things which cause some antennas to accept one wave and reject others:
- The physical size of an antenna influences what wavelength (or what frequency) will be efficiently radiated or received by that antenna.
- The shape of the antenna helps determine the directivity of an antenna. Directivity involves the compass direction at which an antenna radiates or receives EM waves.
- The property of polarization describes the angular pointing of the EM field vector.
All three of these properties (physical size, directivity, and polarization) are separate and distinct properties. The following pages will concentrate on the topic of "polarization".
There are several types of polarization: elliptical, circular, and linear. The polarization type is determined by the angular pointing of the electric field vector.
To determine the polarization type, one imagines observing the tip of the time-varying electric field vector from a fixed point in space along the direction of the wave's propagation (This can be visualized better later). The image traced by this vector tip is usually elliptical, but commonly the ellipse becomes a circle or a straight line.
The following illustration may help in visualizing polarization of EM waves:
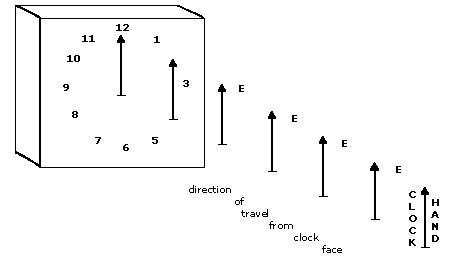
As shown in Figure D-1, we can imagine a clock face with one hand pointing straight up at the 12 o'clock position. Let the hand move out away from the clock face. Immediately after the first hand leaves the clock face, let a second one replace it on the clock and also move out away from the clock face. Repeat this again and again until a steady stream of clock hands are flowing away from the clock, all pointing upward at the same angle. The clock hands are representative of the vector of a vertically polarized electric field as it moves out from the source.
EM waves vary in amplitude during the period of one cycle. This variation repeats over and over again for each cycle of the wave as it is radiated. Let us move ourselves from our viewing position to a new position, one looking at the side of the clock. If we allow each subsequent clock hand (E field vector) to vary in size (amplitude) from the previous one, we get a side view as seen in Figure D-2.
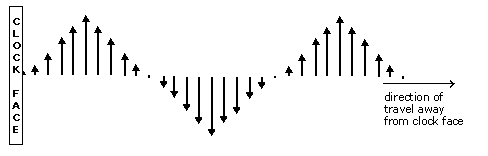
Now we can move back to our original viewing position, as shown in Figure D-1. The vertically pointing clock hand example is comparable to a vertically polarized electric field. If someone were to reach out to catch one of the clock hands, he can catch it only if his hand is positioned at the same angle (polarization) as the clock hand coming broadside at him. Remember the arrows are not pointed at him, but are pointing up and down. If his hand is turned sideways, different from the angle of the clock hands, he would not be able to catch any. If his hand is oriented vertically, he can catch a vertical arrow, but not a horizontal arrow, and conversely.
Just as the pointing of the electric field vector determines the EM field's polarization, the H field is also dependent on the E field's vector. To help see this, add another hand to the clock face so there are now two hands on the clock, perpendicular to each other, as in figure D-3.
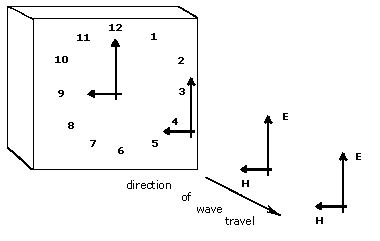
The two clock hands in Figure D-3 represent the E field and the H field vectors. If one hand is positioned at 12 o'clock and is called the E field vector, the other hand to the 9 o'clock position would be the H field vector. The two vectors are at right angles to each other. Since polarization is determined by the E field vector, the illustrated polarization is vertical. (If the E field vector was pointed to the 3 o'clock position, the polarization would be horizontal. If the E field vector is rotating, the polarization is circular or elliptical.) Unlike ordinary clocks, the clock in Figure D-3 requires the two hands always be locked together at a 90 degree angle. The H field vector (illustrated by the 9 o'clock hand) is always perpendicular to the E field vector. The hands can be pointed (tilted) in any direction, but must always be perpendicular to each other. If an antenna's orientation is tilted sideways at an angle, the polarization of the transmitted EM field would tilt by the same angle, but the E and H fields still remain perpendicular to each other.
As explained in the above illustration, the polarization of the EM field is referenced to the E field, with the associated H field at a right angle to the E field. The transmitting antenna determines the polarization angle of the electric field radiated from it. A citizen band (CB) radio antenna pointed straight up would radiate a vertically polarized wave, and a horizontal "dipole" similar to roof mounted TV antennas would radiate a horizontally polarized wave. The best reception is obtained when the receiving antenna is polarized (tilted) to match the polarization of the transmitting antenna. That is why CB antennas all point the same way, straight up.
The following experiment visually demonstrates polarization and the importance of matching the polarization between a source antenna and the receiving antenna:
- Take twopairs of "polarized" sun glasses. They must be polarized.
- Use one pair to filter the light coming from a flashlight.
- Wear the other pair.
- Now tilt your head 90 degrees sideways and notice that one head angle receives the transmitted polarized light and the other receives none.
- Rotate the polarized sun glasses positioned at the light source.
- Now do the head tilts again and notice the polarization angle has changed by the amount rotated in step (e).
NOTE: On a sunny day items on an automobile dashboard can be seen reflected in the windshield, but the images are much less visible if you are wearing polarized sun glasses (provided the windshield is tinted). If you tilt your head while wearing the polarized sun glasses the image reflection will appear and disappear at 90 degree angles.
When performing a non-ionizing radiation survey, the instrument's probe is usually an isotropic receiving antenna. An isotropic probe receives electromagnetic signals regardless of polarization or direction of travel. Such probes are constructed using several antennas arranged in three separate but perpendicular planes. An isotropic probe is designed to give the same reading, no matter which way the isotropic probe is pointed in the EM field.
In conclusion, the clock and arrow illustration presented in this appendix was designed to help the reader understand the difficult concept of polarization. Electromagnetic waves do not actually transfer energy as "arrows" or "small packets" of energy. It would be a mistake to think of RF energy transfer as anything other than a wave whose energy is transferred by the time variation of electromagnetic fields.
REFERENCES
[D1] ANSI/IEEE 100-1984, IEEE Standard Dictionary of Electrical and Electronics Terms, 1984, page 328.
Footnote 1: "X-Rays originate in the extranuclear part of the atom, whereas gamma rays are emitted from the nucleus during nuclear transitions or particle annihilation." Both X-rays and gamma (γ) rays have ionizing effects on tissue. At the same time, in the case of X-rays, " ... the electrons may interact with the nucleus of the atom to produce electromagnetic radiation having a continuous spectrum (bremsstrahlung)." "Gamma rays may also be produced by neutron interactions with nuclei .... the corresponding frequencies are 2x1018 to 2.5x1021 Hz."[3]

